FYZIKÁLNY KOREŠPONDENČNÝ SEMINÁR |
||
| 2. kolo letnej časti 20. ročníka |
|
termín príchodu riešení |
| A-kategória (starší) |
6. 4. 2005 |
|
| školský rok 2004/2005 |
riesenia@fks.sk |
|
| FKS, KZDF MFF UK |
info@fks.sk |
|
| Mlynská dolina, 842 48 Bratislava |
www.fks.sk |
|
|
A-2.1 P(a)lacka (5 bodov)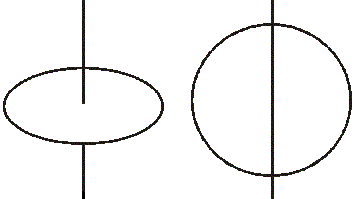 
Majme kruh vyrezaný z homogénneho materiálu s hmotnosťou m a polomerom r. Jeho moment zotrvačnosti vzhľadom na os, ktorá prechádza stredom a je kolmá na rovinu kruhu, je 1/2mr2 (vľavo). Aký je moment zotrvačnosti vzhľadom na os, ktorá prechádza stredom a leží v rovine kruhu (vpravo)? Skúste úlohu vyriešiť bez použitia integrálov. A-2.2 Rádio jádia (5 bodov) 
Jadro rádia Ra22688 , ktoré je v pokoji, sa rozpadá na jadro radónu Rn22286 a časticu α42 (jadro He42). Vypočítajte akou rýchlosťou sa bude pohybovať častica α42 dostatočne dlho po zrážke, keď už môžeme zanedbať vzájomné pôsobenie s Rn22286 . Všetky rýchlosti sú malé v porovnaní s rýchlosťou svetla. Pokojové energie sú v tabuľke. A-2.3 PolE na osi (5 bodov) Vypočítajte veľkosť intenzity E elektrického poľa na osi prstenca s polomerom r nabitého rovnomerne rozmiestneným nábojom Q vo vzdialenosti x od jeho stredu. A-2.4 Priame kmity (5 bodov)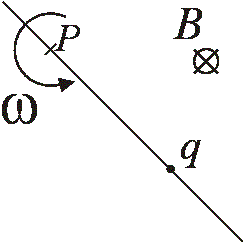 
V medzihviezdnom priestore sa nachádza priamka p ktorá sa otáča okolo svojho bodu P konštantnou uhlovou rýchlosťou veľkosti ω. Celé sa to nachádza v homogénnom magnetickom poli kolmom na rovinu pohybu priamky s indukciou B. Po priamke sa môže bez trenia pohybovať bodový náboj Q s hmotnosťou m. Vedci po dlhom skúmaní zistili, že za istých okolností koná tento náboj harmonické kmity po priamke p s rovnovážnou polohou v bode P. Čo musí spĺňať náboj Q, aby k tomuto javu došlo a aká je perióda týchto kmitov? Tento seminár je organizovaný s podporou | ||
