FYZIKÁLNY KOREŠPONDENČNÝ SEMINÁR |
||
| 3. kolo letnej časti 20. ročníka |
|
termín príchodu riešení |
| A-kategória (starší) |
27. 4. 2005 |
|
| školský rok 2004/2005 |
[email protected] |
|
| FKS, KZDF MFF UK |
[email protected] |
|
| Mlynská dolina, 842 48 Bratislava |
www.fks.sk |
|
|
A-3.1 Trubka (5 bodov) 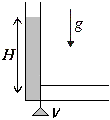
Zvislá trubica je naplnená vodou do výšky H, v spodnej časti je uzavretá ventilom V a ústi do dlhej vodorovnej trubice (táto je na začiatku prázdna). V čase t = 0 ventil otvoríme. Ako závisí rýchlosť klesajúcej hladiny od výšky vody ostávajúcej v zvislej trubici h? Ako sa mení zrýchlenie klesajúcej hladiny s časom t? Pri riešení môžete pokladať polomery trubíc za malé v porovnaní so začiatočnou výškou vody H. A-3.2 Doska levitation (5 bodov) Majme sklenenú dosku s hmotnosťou m, na ktorú začneme kolmo svietiť laserom. Koeficient odrazu pri dopade svetla na rozhranie vákuum-sklo, sklo-vákuum je v oboch prípadoch rovný α. Aký je výkon lasera P, aby sa doska v Zemskom gravitačnom poli nehýbala? Doska je vodorovná a svietime rovno do jej ťažiska. A-3.3 Jednoduchá perióda (5 bodov) 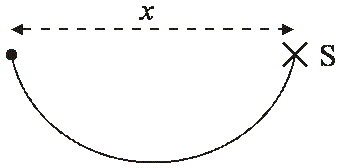
Na nehmotnom, dokonale pružnom, ale nekonečne tuhom vlákne s dĺžkou l, visí hmotný bod, zatiaľ čo druhý koniec vlákna je upevnený v bode S. Hmotný bod zdvihneme do tej istej výšky, v akej sa nachádza bod S a necháme ho voľne padať z vodorovnej vzdialenosti x od S. Nájdite také x rôzne od l, pre ktoré bude náš hmotný bod konať čo najjednoduchší periodický pohyb a vypočítajte jeho periódu. 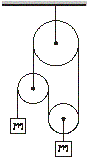
A-3.4 Kladky (5 bodov) Na obrázku je sústava kladiek, ktoré sa môžu otáčať bez trenia a pri výpočte ich môžeme považovať za nehmotné. Aké bude zrýchlenie závaží s hmotnosťami m, ak ich necháme voľne sa pohybovať? Tento seminár je organizovaný s podporou | ||