 |
FX - ročník piaty - leto
| Úvodné slovo a zadania tretej série: | fx5zad3.pdf |
| Introductory note and third series of problems: | fx5zad3en.pdf |
| Zadania štvrtej série: | fx5zad4.pdf |
| Zadania piatej série: | fx5zad5.pdf |
Výsledková listina
| # | Riešiteľ | FX7 | FX8 | FX9 | FX10 | FX11 | FX12 | FX13 | FX14 | FX15 | sum |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Jakub Kocák | 7 | 9 | 9 | 9 | 9 | - | 9 | 9 | 0 | 61 |
| 2. | Eugen Hruška | 9 | 9 | 9 | 9 | 4 | 0 | 9 | 5 | - | 54 |
| 3. | Andrej Vlček | 4 | 4 | - | - | 4 | - | 9 | - | - | 21 |
| 4. | Ján Pulmann | 9 | - | - | - | - | - | - | 4 | - | 13 |
| 5. | Jakub Šafin | - | 2 | - | - | - | - | 7 | 1 | - | 10 |
| 6. | Vladimír Macko | 1 | - | - | - | - | - | - | - | - | 1 |
Zadania príkladov letnej časti piateho ročníka:
FX7 Puk (opravuje Petrík)
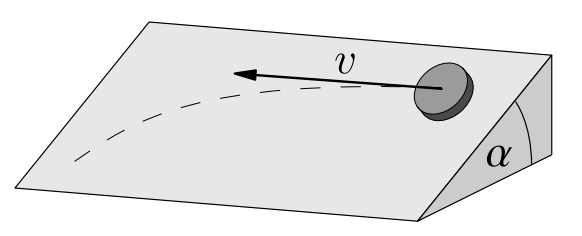
Mirka našla v skrini nekonečne veľkú naklonenú rovinu so sklonom α a puk. Koeficient trenia medzi pukom a naklonenou rovinou je f = tg α. Mirka umiestnila puk na naklonenú rovinu a udelila mu rýchlosť v v horizontálnom smere. Aká bude rýchlosť puku po dostatočne dlhom čase?
FX8 Vločka (opravuje Marika)
Polik sa rozhodol vyzdobiť si izbu farebnými obrázkami. Preto vzal nožničky a vystrihol si z farebného papiera niekoľko fraktálov, konkrétne
a) Sierpinského trojuholník
b) Kochovu vločku
s hmotnosťou m a dĺžkou hrany a. Zaujíma ho, aký je moment zotrvačnosti jeho výstrižkov. Pomôžete mu?

FX9 Siločiara (opravuje Bzdušo)
Škrekovi prišli poštou dva rovnaké bodové náboje +Q. Plný nadšenia ich
umiestnil do vzdialenosti d od seba a zahľadel sa na siločiaru, ktorá pod
uhlom α k spojnici nábojov vychádza z jedného z nich. Aký je smer tejto siločiary vo veľmi veľkej vzdialenosti od nábojov?
FX10 Trubice (opravuje Filip)
Bubo vzal dve rovnaké trubice a zamuroval ich do (nekonečne veľkej) steny hrúbky H a s tepelnou vodivosťou λ tak, že stenou prechádzajú kolmo a ich stredy sú vo vzájomnej vzdialenosti λ. Jednou trubicou nechal pretekať teplú vodu, ktorá do steny privádza tepelný výkon P, druhou nechal pretekať studenú vodu, ktorá zo steny tepelný výkon P odoberá. Bubo má niekoľko otázok o teplote steny v ustálenom stave:
a) Dokážte, že izotermy (t.j. miesta s rovnakou teplotou) steny majú profil kružnice!
b) Nájdite teplotu bodu steny, ktorý sa nachádza vo vzdialenostiach r1,r2 od stredov trubíc a pre +Q1,2 rádovo väšie ako d ju vyjadrite pomocou polárnych súradníc (r,φ).
Rovnica vedenia tepla je h=-λ∇T, kde h je tepelný tok. Tepelnú výmenú s okolitým vzduchom, ako aj tepelné vyžarovanie, neuvažujte!
FX11 Synchronizované blikanie (opravuje Juro)
Marcel to po roku znova prehnal s pozeraním Star Trek-u. Tento raz sa mu snívalo, že sa do vesmíru vydal spolu s Marekom v dvoch rôznych raketách. Obaja vyštartovali naraz rovnako veľkými rýchlosťami v vzhľadom na Zem, avšak opačnými smermi. Keď boli ich rakety (v sústave Zeme) od seba vzdialené L, Marcel zablikal reflektorom na svojej rakete. Marek potom zablikal tiež a to súčasne (vo svojej vzťažnej sústave) s Marcelom. Marcel zablikal druhý raz súčasne (vo svojej vzťažnej sústave) s Marekovým prvým zablikaním atď. Ako ďaleko sú rakety od seba z pohľadu pozorovateľa na Zemi v okamihu, keď Marcel zabliká po n-tý raz?
FX12 Marsrobot II. (opravuje Jakub)
Po prvom úspechu modelu Marsrobota v 1. letnej sérii FKS 25. ročníka sa tento výrobok dostal už aj do tvrdších testov. Uvažujme robota s nasledovnými vlastnosťami:
(i) Polomer robota je R, jeho celková hmotnosť M.
(ii) Závažie je na nehmotnej dĺžky dĺžky r<R a samotné má hmotnosť m.
(iii) Telo robota aj s motorčekom je rotačne symetrické okolo stredovej rovnobežnej osi. Moment zotrvačnosti okolo tejto osi je IS a nezávisí od činnosti motorčeka.
(iv) Robot neprešmykuje.
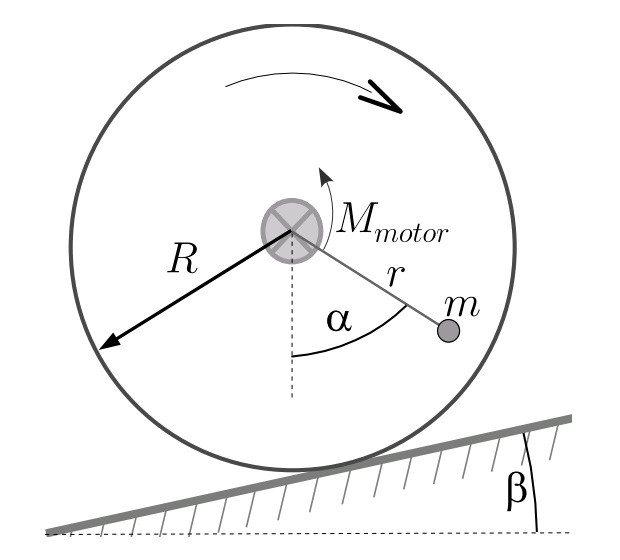
a) Majme dráhu (obrázok je v pdf-zadaniach), ktorá pozostáva z vodorovného úseku dĺžky l a z troch oblúkových častí rôznych polomerov, pričom platí, že R<R1,2,3. Robot na začiatku stojí na začiatku rovného úseku. Urč o aký celkový uhol sa robot otočí, kým príde do miesta s maximálnym stúpaním.
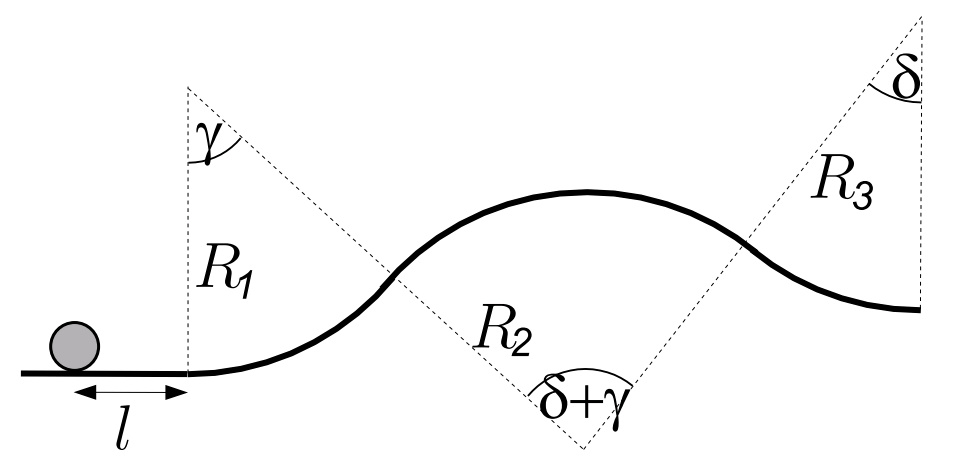
b) Spočítajte okamžité uhlové zrýchlenie robota. Vyjadrite ho pomocou týchto veličín: uhlového zrýchlenia robota pomocou týchto veličín: uhlová rýchlosť robota ω, uhol &\alpha; a jeho uhlová rýchlosť Ω, aktuálne stúpanie β, lokálny polomer krivosti povrchu ρ a moment sily motorčeka Mmotor vzhľadom na stred robota.
c Pre hodnoty R = 1 m, r = 0,8 m, M = 100 kg, m = 10 kg, IS = (M-m)*R2/2 = 45 kg.2, g = 10 m.s-2, k = 4 m, R1 = 5 m, R2 = 25 m, R3 = 15 m, γ = 8°, δ = 5° vyriešte numericky pohyb robota ak viete, že robot na začiatku stál a závažie voľne viselo. V čase po štarte až po dosiahnutie najvyššieho bodu dráhy motor robota pracoval s konštantným momentom Mmotor = 40 N. Po dosiahnutí vrcholu dráhy motor prestal pracovať. Ako výstup chceme od vás čas, kedy robot prechádzal koncom dráhy. Určte tiež celkovú prácu, ktorú motorček vykonal. Určte aj rozdiel mechanickej energie na konci a na začiatku.
Poznámka: Táto úloha je náročná. Časti (a) a (c) vám môžu pomôcť -- ak si však trúfate, tak ich nemusíte riešiť, stačí mi výsledok (b).
Hinty: Časť (a) si treba poriadne nakresliť, inak nie je ťažká. Časť (b) je najťažšia, treba zúročiť časť (a). Numerické riešenie vám môže pomôcť odhaliť prípadné chyby urobené v časti (b). Zjemňovaním časového kroku simulácie by ste mali dostávať presnejšie riešenia.
FX13 Pravítko (opravuje Bzdušo)
Kika si všimla, že jej trojuholníkové pravítko kmitá pri zavesení za ľubovoľný vrchol s rovnakou periódou. S tou istou periódou kmitá dokonca aj vtedy, keď ho zavesí za stred prepony dĺžky d. Ozaj, s akou?
FX14 Supravodivá rovina (opravuje Peťo)
Peťo našiel vo vesmíre nekonečnú supravodivú rovinu. Vyvŕtal do nej veľmi malý otvor a do vzdialenosti h kolmo nad ním vložil bodový náboj Q s hmotnosťou m. Keď náboj pustil, začal sa periodicky pohybovať. Vysvetlite prečo a určte periódu tohto pohybu.
Hrúbku roviny považujte za zanedbateľnú. Magnetické javy v dôsledku pohybu náboja a indukovaných prúdov neuvažujte.
FX15 Most II. (opravuje Jakub)
V 2. letnej sérii FKS 25. ročníka sme riešili úlohu o moste cez Dunaj. Teraz
budeme riešiť o niečo všeobecnejšiu úlohu. Treba preklenúť rieku šírky
L = 300 m. Most má mať jediný pilón umiestnený na brehu rieky, ktorý
tentoraz nemusí byť rovný (a ani rovnakého prierezu). Na vás je, aby most
nespadol a pritom nebol ani priveľmi nákladný -- Treba navrhnút tvar piliera
tak, aby žiadne napätia v materiáloch
neprevýšili pätinu ich medze pevnosti, a zároveň, aby bola cena mostu
minimálna možná.
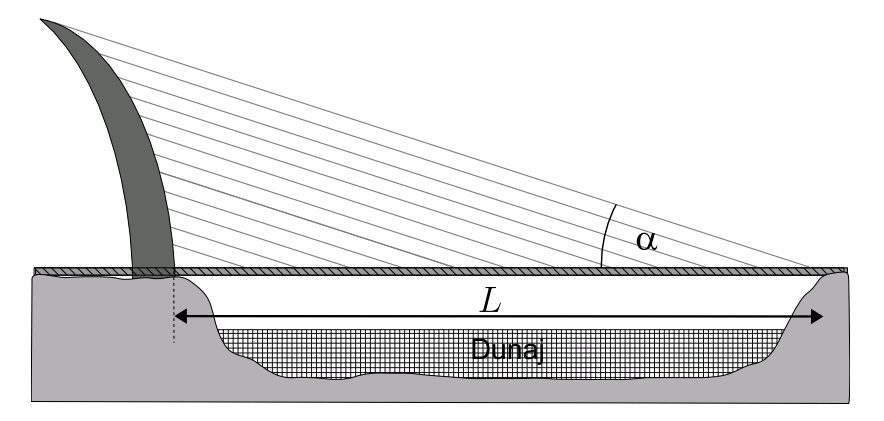
Most bude mat betónovú mostovku (to, po čom jazdia autá) a pilier, a oceľové
laná. Hmotnosť 1 metra mostovky aj s uvažovanou premávkou (autá) na
nej je 20 ton. V predošlom príklade vo FKS sme ukázali, že hmotnosť
lanovia je zanedbateľná voči hmotnosti mostovky -- Možno predpokladať, že tomu
bude aj tu tak a teda počítať treba v aproximácii nehmotných lán (voči
hmotnosti mostovky). Konštrukcia je vymyslená tak, že pilier a aj mostovka
môžu byť v každom mieste zaťažené iba v pozdĺžnom smere (nemá v nich byť
šmykové napätie). Oceľové laná sú veľmi husto rozmiestnené a navzájom
rovnobežné.
Potrebné údaje: Hustota betónu ρbetón = 2000 kg.m-3,
hustota ocele ρoceľ = 7800 kg.m-3, medza pevnosti
betónu v tlaku σbetón = 40 MPa, medza pevnosti ocele
v ťahu σoceľ = 2 GPa. Cena ocele za jednotku
hmotnosti je 47-násobok ceny betónu rovnakej hmotnosti.
Novinky
Máme novú stránku!
Letný tábor Trojstenu sa bude konať 15. až 24. augusta. Prihlás sa na ltt.fks.sk!
27. 7. - 7. 8. sa bude konať Letná škola FKS a TMF
Pripravili sme pre vás posledné tohtoročné vzoráky 3. letnej série!
Máme tu 4. sériu FX!
Napiekli sme pre vás už aj zadania 3. letnej série!
Je tu už dlho ... ale stále je úžasná a aktuálna ... Zbierka FX |
Kalendár |