 |
FX - ročník ôsmy - leto
| Úvodné slovo a zadania tretej série: | fx8zad3.pdf |
| Zadania štvrtej série: | fx8zad4.pdf |
Výsledková listina
| # | Riešiteľ | FX7 | FX8 | FX9 | FX10 | FX11 | FX12 | sum |
|---|---|---|---|---|---|---|---|---|
| 1. | Jakub Šafin | 9 | 9 | 9 | 9 | 2 | 9 | 47 |
| 2. | Patrik Turzák | 9 | 9 | 4 | 9 | - | 9 | 40 |
| 3. | Ján Ondráš | 9 | 9 | 4 | 6 | 0 | - | 28 |
| 4. | Dušan Kavický | 7 | 9 | 4 | - | - | - | 20 |
| 5. | Tomáš Gonda | 4 | 5 | 5.5 | - | - | - | 14.5 |
| 5. | Jakub Bahyl | 4 | 5 | 5.5 | - | - | - | 14.5 |
| 7. | Karolína Šromeková | 5 | 9 | - | - | - | - | 14 |
| 8. | Matej Badin | - | 9 | - | - | - | - | 9 |
| 9. | Lýdia Janitorová | - | - | 4.5 | 0 | - | - | 4.5 |
Zadania príkladov letnej časti ôsmeho ročníka:
FX7 Granát (opravuje Jakub Ko.)
Predstavte si nasledovný experiment: Európska vesmírna agentúra umiestni do istej vzdialenosti od Slnka (nehybný) granát. V istom momente vybuchne a úlomky granátu sa rozletia do všetkých možných smerov rýchlosťou veľkosti v. Ukážte, že
- všetky úlomky budú okolo Slnka obiehať po eliptických dráhach s rovnako veľkou hlavnou polosou,
- množina všetkých bodov v priestore, do ktorých sa nejaký úlomok niekedy dostane, tvorí plný elipsoid.
FX8 Mravčeky (opravuje Jakub)
Táto úloha sú v skutočnosti úlohy dve!
Časť [A]
Kaja vzala gumu počiatočnej dĺžky L. Jeden jej koniec upevnila k stene a druhým koncom začala gumu naťahovať tak, že jej dĺžka v čase t je L+ut. Súčasne s naťahovaním sa po gume začal od steny pohybovať mravec konštantnou rýchlosťou v. Zistite, aká musí byť rýchlosť v, aby sa mravcovi podarilo prísť na opačný koniec gumy a ako dlho mu to bude trvať! Predpokladajte, že guma sa naťahuje rovnomerne a možno ju natiahnuť na ľubovoľnú dĺžku.
Časť [B]
Predstavte si svet tvaru dvojrozmernej roviny (volajme ho "horúca platnička") na ktorom žiju dvojrozmerné bytosti -- mravčeky. Mravčeky ako aj všetky ich nástroje sú vyrobené z materiálu s rovnakou teplotnou rozťažnosťou α, všetky objekty sa tu naťahujú podľa L=α T L0. Keď sa mravček presunie na teplejšiu oblasť platničky, on aj jeho nástroje sa zväčšia rovnako veľmi, takže rozťahovanie vôbec nepostrehne.
Čudnosť svojho sveta však mravčeky môžu objavovať inak -- geometricky! Keďže úsečky definované ako najkratšie spojnice dvoch bodov sú akosi krivé (oplatí sa ísť cez teplejšie oblasti, kde sú pravítka dlhšie), nemalo by byť prekvapivé, že súčet vrcholových uhlov v trojuholníku tu nemusí byť 180° alebo že pokus o nakreslenie štvorca, t.j. série čiar rovnakej dĺžky postupne na seba kolmých, tu môže zlyhať.
Vaša úloha je nasledovná: Ako má vyzerať teplotná mapa platničky, aby geometria na nej bola identická s geometriou na guli? (Myslí sa to okrem jej južného pólu, ktorý sa na našu platničku \uv{nevzmestí}.)
FX9 Zápalky (opravuje Halucinka)
Vo fyzike existuju dve rôzne interpretácie pravdepodobnosti, tzv. frekvencionistická, a bayesovká. Tá prvá chápe pravdepodobnosť nejakého javu ako objektívnu veličinu, ktorú možno určiť dostatočne veľkým počtom experimentov. Druhá chápe pravdepodobnosť ako subjektívnu veličinu zohľadňujúcu naše množstvo vedomostí o danom fyzikálnom jave. Zatiaľčo tá prvá je známa zo stredoškolskej matematiky, vo fyzike sa čoraz častejšie využívajú deduktívne metódy založené na tej druhej. Táto úloha vás s ňou trochu oboznámi.
Centrálnymi pojmami bayesiánskeho prístupu sú apriórna a aposteriórna pravdepodobnosť. (Z latinského a priori (na základe predošlého) a a posteriori (na základe neskoršieho).) Apriórna pravdepodobnosť vyjadruje naše predpoklady pred vykonaním experimentu a aposteriórna vyvinuté predstavy vyplývajúce z apriórnej pravdepodobnosti a výsledkov experimentu. Ústredná je rovnica pre podmienené pravdepodobnosti, ktorú odôvodnil anglický duchovný Thomas Bayes. Znie
V tejto rovnici sú P(Aj) a P(B) pravdepodobnosti dvoch náhodných javov Aj a B, P(B|Aj) je podmienená pravdepodobnosť javu B ak nastal jav Aj$. Veličina P(Aj|B) určuje podmienenú pravdepodobnosť javu Aj ak nastal jav B.
Vo fyzikálnom žargóne sa javy Aj a B môžu nazvať teória a experiment. V tom prípade P(Aj) vyjadruje apriórnu pravdepodobnosť, že teória Aj je pravdivá, P(B|Aj) je pravdepodobnosť že teória Aj dá experimetálny výsledok B, P(B)=∑j P(B|Aj) P(Aj) je pravdepodobnosť, s akou podľa našich vedomostí vôbec nastane jav B. Potom P(Aj|B) vyjadruje, s akou pravdepodobnosťou je teória Aj pravdivá po zohľadnení experimentu B.
Všimnite si, že táto interpretácia je kompatibilná s oboma extrémami: Ak sme si istí, že nejaká teória Aj určite nie je pravdivá a vopred ju vylúčime, P(Aj)=0, tak aj P(Aj|B)=0, t.j. žiadne experimentálne dáta nás o teórii Aj neprinútia uvažovať. Naopak, ak sme si od začiaku istí, že teória Aj je určite pravdivá (čiže vopred vylúčime všetky ostatné teórie), tak podľa rovnice nás žiadne experimentálne výsledky neprinútia pochybovať. Presvedčte sa!
Táto úloha pozostáva z troch praktických problémov zo života, fyziky je tu naozaj málo. Prvé dve úlohy sú zahrievacie, tá posledná je naozajstná.
Problém [A]
V istom meste sa stala nehoda -- v nočných hodinách bol chodca zrazený taxíkom. Podľa očitého svedka išlo o oranžový taxík. Polícia vie, že v meste je 900 taxíkov žltých, zvyšných 100 taxíkov je oranžových. Testy v svetelných podmienkach zodpovedajúcim tým v čase nehody ukázali, že očitý svedok identifikuje žltý taxík s pravdepodobnosťou $18\%$ ako oranžový a s $5\%$ oranžový ako žltý. Ako zmenilo domnienky o páchateľovi toto očité svedectvo? Je dôvod predpokladať, že nehodu naozaj spôsobil oranžový taxík??
Problém [B]
Istou chorobou trpí 1% populácie. Bežne používaný test s pravdepodobnosťou 95% chorobu správne diagnostikuje resp. vylúči, vo zvyšných 5% prípadov diagnostikuje chorobu klinicky zdravým ľuďom resp. neodhalí ju u chorých. Ak vám takýto test oznámi, že ste chorí, s akou pravdepodobnosťou ste naozaj chorý? Ako sa vaša vedomosť zmení, ak aj druhý nezávislý test potvrdí vašu chorobu? Predpokladajte, že druhý test má rovnakú spoľahlivosť a že jeho výsledky sú nekorelované s výsledkami prvého testu.
Problém [C]
Eva si v obchode kúpila 10 krabičiek so zápalkami. Po rozbalení zistila, že tri z nich majú na obrázku Glärnisch, dve Wetterhorn, dve Matterhorn, dve Piz Beverin a jedna Jungfrau. Aký počet rôznych existujúcich vzorov možno očakávať na základe Evou náhodne vybranej desatice? Predpokladáme, že výrobca vyrába všetky vzory v rovnakom počte. Pred experimentom s rovnakou pravdepodobnosťou prípušťame všetky možné počty rôznych vzorov.
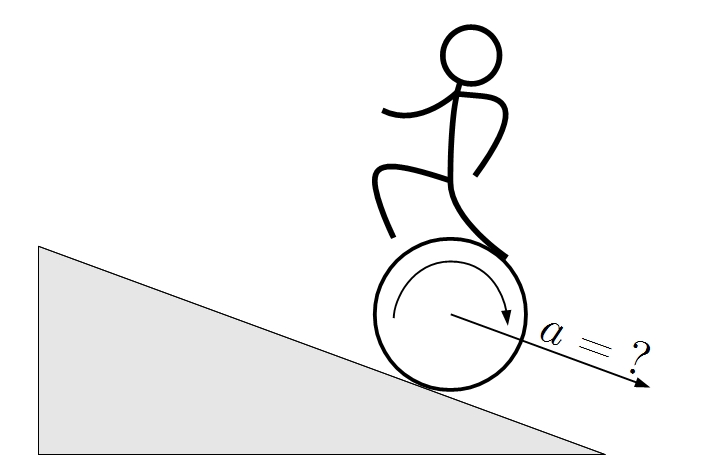
FX10 Kotúľ (opravuje Marcelka)
Paťo (s hmotnosťou m) trénuje cirkusové vystúpenie. Jeho kúsok spočíva v tom, že sa postaví na prázdny sud (s hmotnosťou M a momentom zotrvačnosti MR2) a nechá ho kotúlať sa dolu naklonenou rovinou so sklonom α. Paťo pritom po sude beží tak, že sa stále nachádza na jeho najvrchnejšom bode. Zistite s akým zrýchlením sa za týchto okolností sud kotúľa. Predpokladajte, že sud na podložke neprešmykuje!
FX11 Dvojité kyvadlo (opravuje Tomáš)
Zadanie pre géniov:
Vyriešte problém dvojitého matematického kyvadla pomocou princípu minimálneho účinku, ktorý použijete numericky.
Zadanie pre normálnych ľudí:
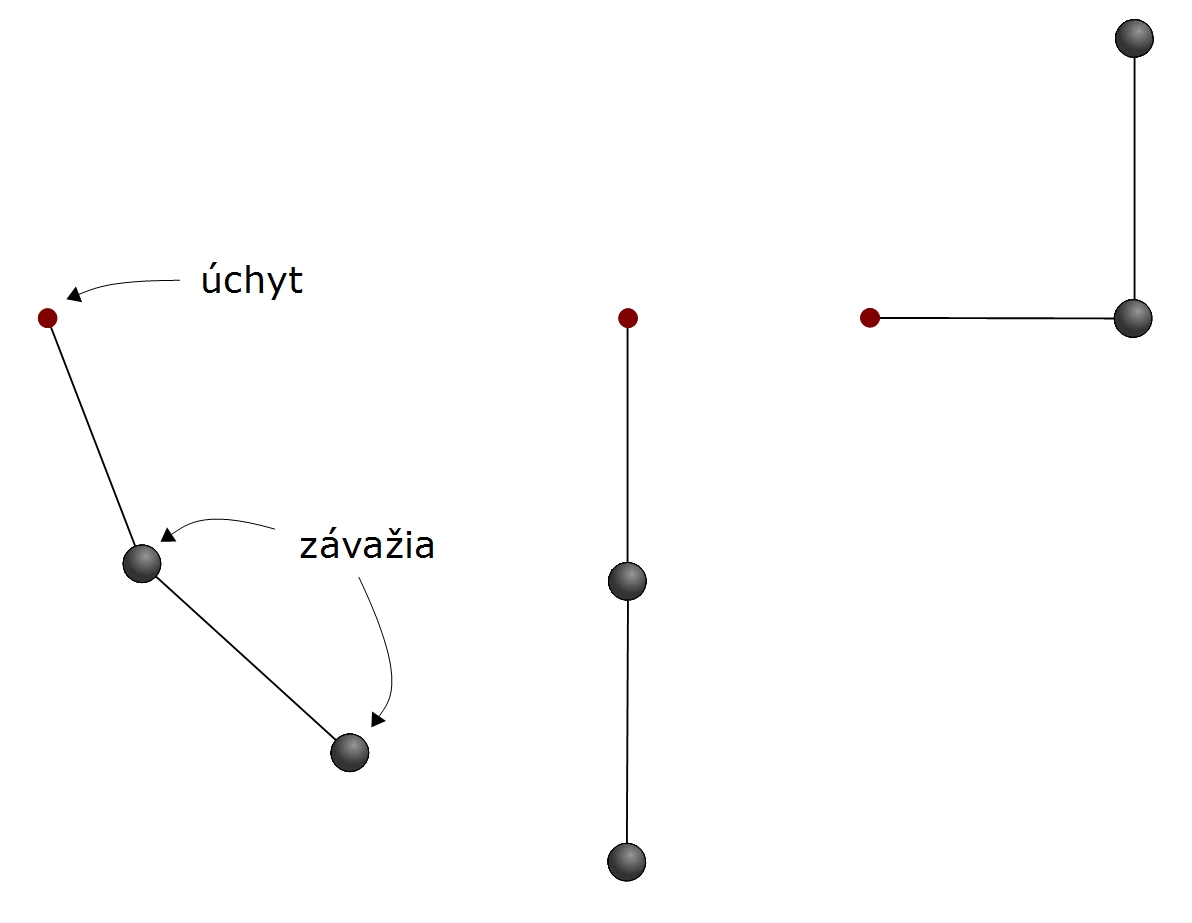
Princíp minimálneho účinku hovorí, že telesá sa snažia pohybovať tak, aby priemerná hodnota rozdielu ich kinetickej a potenciálnej energie za daný čas bola čo najnižsia. Tento čudesný zákon dokáže nahradiť pohybové rovnice, avšak na praktické výpočty sa používa zriedka. Týmto príkadom sme sa rozhodli tento neduh napraviť. Viac o princípe nájdete TU. Dvojité matematické kyvadlo si možno predstaviť ako dve matematické kyvadlá pod sebou, viď ľavý z trojice obrázkov.
Presné zadanie vašej úlohy:
Na prostrednom obrázku je zachytená poloha kyvadla v čase 0s, na pravom v čase 10 s. Dĺžka oboch tyčí je 20 cm, hmotnosť oboch závaží 100 g, gravitačné zrýchlenie 10 m.s-2. Trenie neuvažujeme. Aké musia byť rýchlosti závaží v čase 0 s na obrázku vľavo, aby bol takýto vývoj možný?
- Nájdite čo najviac možných dvojíc v1, v2, ktoré sú riešením úlohy.
- Najexotickejší pohyb, ktorý nájdete, vizualizujte a zaveste na YouTube, link vložte do riešenia.
Návod:
- Postupujte numericky, otvorte si Python / Javu / C / Ruby / JavaScript / Matlab / Excel a smelo do toho.
- Ak ste si z predchadzajucej ponuky vybrali Excel, vráťte sa na krok 1.
- Spustite Python.
- Vymyslite, ako čo najjrozumnejšie reprezentovať vývoj kyvadla (teda, nie len okamžitý stav, ale celý vývoj od času 0 s po čas 10 s.
- Zrátajte pre tento vývoj účinok.
- Skúste jemne poštelovať s vývojom a nájsť nový vývoj s menším účinkom.
- Automatizovane opakujte niekoľko posledných krokov, až kým nedostanete vývoj s lokálne minimálnym účinkom, ktorý už neviete vylepšiť.
Pár ďalších rád:
- Nakóďte si jednoduchú vizualizáciu výsledného optimálneho vývoja, silne to odporúčam. Jednak uvidíte, či vám to ráta dobre a dvak, robí to úžasné veci.
- Neprepadajte panike!.
- Spustite Python.
- Zabudnite na prežitky ako sú pohybové rovnice. Pri princípe minimálneho účinku vás nesmie trápiť, že vývoj, s ktorým pracujete, im odporuje. Je dokázané, že pokiaľ nájdete vývoj s minimálnym účinkom, tento bude ok aj čo do klasických pohybových rovníc.
- Ak máte problémy so zachytávaním videa, pokojne nahrajte fotoaparátom váš monitor, postačí to.
- Vaše video môže byť oproti realite spomalené, aspoň bude lepšie sledovateľné.
- Najexotickejší pohyb vyhráva od Andreja kompót.
FX12 Magnet (opravuje Janči)
V tejto úlohe sa oboznámime s najjednoduchšou mikroskopickou teóriou popisúcou fázový prechod - metódou stredného poľa. Budeme ju aplikovať na zjednodušený, tzv. klasický Isingov model magnetu. Je na mieste vopred upozorniť, že výsledky tejto teórie sú veľmi odlišné od experimentálnych meraní pre naozajstné magnety. Existujú však iné fázové prechody prvého druhu, pre ktoré teória funguje s úžasnou presnosťou (napr. prechod kovov do supravodivého stavu pri nízkych teplotách - to síce nie je obsahom tejto úlohy, ale v samom závere sa k tejto zaujímavosti vrátime).
Než vysvetlím, čo metóda stredného poľa znemaná, predstavím už spomínaný klasický Isingov model magnetu. Predstavte si kubický kryštál, v ktorom je rozmiestnených n × n × n ≡ N elementárnych magnetov, tzv. spinov, ktoré sa môžu nachádzať v dvoch stavoch: Hore (↑ alebo +1) a dole (↓ alebo -1). Dovedna teda existuje 2N rôznych mikroskopických konfigurácií. Energia konfigurácie je daná vzťahom
kde si = ± 1 je orientácia spinu v mriežkovom bode i, B je externé magnetické pole, J>0 popisuje silu feromagnetickej interakcie spinov a ∑⟨i,j⟩ značí sčitovanie cez dvojice najbližších susedov. V uvažovanom trojrozmernom kryštáli má každý spin šesť najbližších susedov.
Zo štatistickej fyziky vieme, že každá z množstva konfigurácii sa v systéme realizuje s pravdepodobnosťou úmernou e-Ekonfig./kBT, tzv. Boltzmannov zákon. Očakávaná hodnota fyzikálnej veličíny A sa potom počíta ako stredná hodnota
kde Akonfig. je hodnota veličiny A ak sa realizuje konkrétna konfigurácia a obe sumy bežia cez všetkých 2N možných konfigurácií systému. Tu však narážame na dva problémy: Prvý, zmagnetizovaný materiál bez vonkajšieho poľa na rozumných časových škálach, povedzme na škálach porovnateľných s vekom vesmíru, nemení svoju os magnetizácie. Fluktuácia, ktorá by magnet prepólovala totiž stojí veľa energie a je extrémne málo pravdepodobná. Magnet sa teda nedostane do všetkých možných konfigurácii a sumy treba nejako orezať. Druhý problém je celkom očakávateľný - sumy v rovniciach nevieme vypočítať.
Metóda stredného poľa} je drastickým zjednodušením. Predpokladá sa, že každý spin interaguje s priemernou magnetizáciou celého kryštálu. Keďže 6 <<< N3, nemožno očakávať zázraky - najmä pokiaľ sa v magnete realizujú korelácie na vzdialenostiach väčších ako vzdialenosť druhých najbližších susedov. Skutočne, sú to práve zanedbané flukuácie, kvôli ktorým nedáva metóda stredného poľa dobré predpovede. Metóda však aspon kvalitatívne vysvetľuje existenciu fázového prechodu a hysterézne správanie magnetov. To si ukážeme.
Postupujte nasledovne: Nech ⟨s⟩ = ∑i si ⁄ N značí priemernú orientáciu spinu v kryštáli. Tú pre dané parametre T, B vopred nepoznáme, čo nám neprekáža ju nejako označiť. Zrejme ⟨s⟩ ≠ 0 bude znamenať magnetický stav kryštálu. Obmedzte sa na jediný spin ktorého 6 susedov nahraďte stredným poľom ⟨s⟩. Boltzmannovským prístupom určite, s akou pravdepodobnosťou sa tento spin nachádza v stavoch ±1 a aká je jeho stredná magnetizácia. Požadovaním "konzistentnosti", t.j. že stredná hodnota skúmaného spinu je rovnaká ako priemerná magnetizácia vstupujúca do výpočtu, ukážte že môžu nastať nasledovné prípady:
- Ak B = 0 a T je väčšia ako istá medzná (tzv. kritická alebo Curieho) teplota Tc, tak existuje jediné riešenie ⟨s⟩ = 0, nemagnetický stav.
- Ak B = 0 a T<Tc, existujú riešenia ⟨s⟩ = 0 a ±⟨s⟩ ≠ 0. Ukážte, že magnetický stav má nižšiu energiu ako nemagnetický a numericky určte závislosť nenulového ⟨s⟩ od teploty.
- Ak B ≠ 0, môže existovať jedno až tri riešenia. Ukážte, že vo všeobecnosti sú všetky tri nenulové a dajte im fyzikálnu interpretáciu.
Ďalej ukážte, že pre T<Tc a existuje kritická veľkosť magnetického poľa Bc ktorá spôsobí premagnetizovanie systému a že prekročenie tohto magnetického poľa povedie na hysterézne správanie.
Fázové prechody sú charakterizované sadou tzv. kritických exponentov. Hoci vo fyzike existuje veľké množstvo fázových prechodov, na základe sady hodnôt kritických parametrov ich možno všetky klasifikovať do prekvapivo malého množstva tried, tzv. univerzalít. Napríklad kritické exponenty nášho modelu magnetu v priblížení stredného poľa sú identické s kritickými exponentami supravodiča. Ďalším príkladom je kondenzácia plynu, ktorá patrí do tej istej triedy ako presné riešenie klasického Isingovho modelu.
Toto sú definície niektorých kritických exponentov:
- Ak teplota T je blízka Tc, tepelná kapacita sa škáluje ako C ∼ |T-Tc|α.
- Ak teplota T je o málo menšia ako Tc, tak magnetizácia sa škáluje ako ⟨s⟩ ∼ (Tc -T)β.
- Ak T = Tc, magnetizácia závisí od externého magnetického poľa ako ⟨s⟩ ∼ B1/δ.
Určte exponenty α, β a δ v priblížení stredného poľa.
Poznámka: Pri popise kvapalín a supravodičov sa magnetizácia nahradzuje inou veličinou, tzv. parametrom usporiadania, ktorá je v týchto fázach nenulová a vo vysokoteplotnej fáze je nulová. V definíciách kritických parametrov pre tieto fázové prechody treba spraviť tú istú zámenu magnetizácie za parameter usporiadania.
Novinky
Máme novú stránku!
Letný tábor Trojstenu sa bude konať 15. až 24. augusta. Prihlás sa na ltt.fks.sk!
27. 7. - 7. 8. sa bude konať Letná škola FKS a TMF
Pripravili sme pre vás posledné tohtoročné vzoráky 3. letnej série!
Máme tu 4. sériu FX!
Napiekli sme pre vás už aj zadania 3. letnej série!
Je tu už dlho ... ale stále je úžasná a aktuálna ... Zbierka FX |
Kalendár |